Leetcode 141 Linked List Cycle

Soru

Given head, the head of a linked list, determine if the linked list has a cycle in it.

There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail’s next pointer is connected to. Note that pos is not passed as a parameter.

Return true if there is a cycle in the linked list. Otherwise, return false.

Follow up: Can you solve it using O(1) (i.e. constant) memory?

Örnek 1

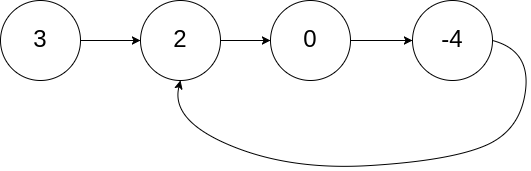
Input
Input: head = [3,2,0,-4], pos = 1
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).

Örnek 2

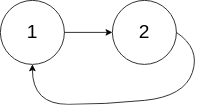
Input: head = [1,2], pos = 0
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 0th node.

Örnek 3

Input: head = [1], pos = -1
Output: false
Explanation: There is no cycle in the linked list.

Çözüm

• Bir bağlı listenin (linked list) döngü içerip içermediğini kontrol etmenizi ister. Bu problem, bir bağlı liste verildiğinde, listenin herhangi bir noktasında düğümlerin tekrar başa dönüp dönmediğini (yani döngü oluşturup oluşturmadığını) belirlemenizi gerektirir.
• Girdi: Bir bağlı listenin baş düğümü (head).
• Çıktı: Eğer liste bir döngü içeriyorsa true, aksi takdirde false.
• Bu problemi çözmek için yaygın kullanılan iki yöntem vardır: Floyd’un Çevrim Tespiti Algoritması (tortoise and hare algoritması) ve Hash Tablosu kullanımı.
• Floyd’un Çevrim Tespiti Algoritması (Hare and Tortoise): Bu yöntemde, iki işaretçi (pointer) kullanılır: biri yavaş (tortoise) diğeri hızlı (hare). Yavaş işaretçi her adımda bir düğüm, hızlı işaretçi her adımda iki düğüm ilerler. Eğer liste içinde bir döngü varsa, bu iki işaretçi bir noktada kesinlikle karşılaşacaktır. Karşılaşmaları, döngünün varlığını gösterir.
• Hash Tablosu Kullanımı: Bu yöntemde, ziyaret edilen düğümler bir hash tablosunda veya sette saklanır. Her düğüm ziyaret edildiğinde, bu düğüm daha önce ziyaret edilmiş mi diye kontrol edilir. Eğer bir düğüm daha önce ziyaret edilmişse, bu bir döngü olduğunu gösterir.
• Çalışma Mekanizması:
• İşaretçilerin İnitialize Edilmesi: slow başlangıçta baş düğümde, fast ise baş düğümün bir sonraki düğümünde başlar.
• Döngü: slow her adımda bir düğüm, fast her adımda iki düğüm ilerler. Eğer fast veya fast.next None olursa, bu listenin sonuna ulaşıldığını ve döngü olmadığını gösterir.
• Sonuç: Eğer slow ve fast işaretçileri aynı düğümde buluşursa, liste içinde bir döngü olduğu anlamına gelir.

Code

class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next

class Solution:
    def hasCycle(self, head):
        if not head:
            return False
        
        slow = head
        fast = head.next
        
        while slow != fast:
            if not fast or not fast.next:
                return False
            slow = slow.next
            fast = fast.next.next
        
        return True

Complexity

• Time complexity (Zaman Karmaşıklığı): O(n), burada n düğüm sayısıdır. En kötü durumda tüm düğümleri ziyaret edebiliriz.
• Space complexity (Alan Karmaşıklığı): O(1) Floyd’un Çevrim Tespiti Algoritması için, çünkü ekstra bir alan kullanılmaz. Hash tablosu kullanıldığında alan karmaşıklığı O(n) olur.