Leetcode 226 Invert Binary Tree
Soru
Given the root of a binary tree, invert the tree, and return its root.
Örnek 1
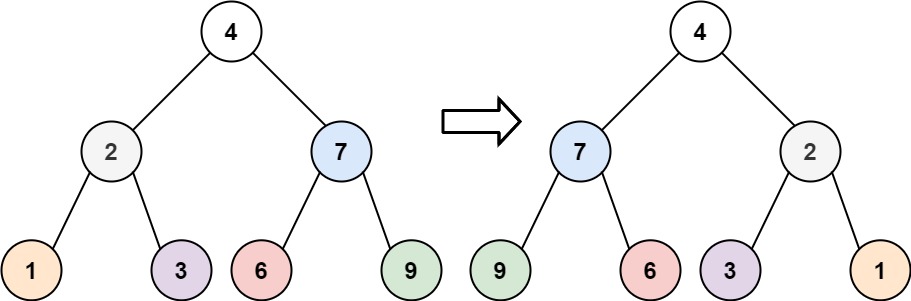
Input: root = [4,2,7,1,3,6,9]
Output: [4,7,2,9,6,3,1]
Örnek 2

Input: root = [2,1,3]
Output: [2,3,1]
Örnek 3
Input: root = []
Output: []
Çözüm DFS
- “226. Invert Binary Tree” sorusu, bir ikili ağacı tersine çevirmenizi ister. Bu problemde, verilen bir ikili ağacın tüm alt ağaçlarını yer değiştirerek ters çevirmeniz gerekiyor; yani, her düğümün sol çocuğu sağ çocuğuyla ve sağ çocuğu sol çocuğuyla yer değiştiriyor. Bu işlem, ağacın en üst düzeyinden en alt düzeyine kadar rekürsif olarak uygulanır.
- Girdi: İkili bir ağacın kök düğümü (root).
- Çıktı: Aynı ikili ağacın tersine çevrilmiş hali.
- Bu problem genellikle özyinelemeli (recursive) veya yinelemeli (iterative) yöntemler kullanılarak çözülür. Her iki yöntem de ağacın her düğümünü ziyaret eder ve sol ve sağ çocukları yer değiştirir.
- Çalışma Mekanizması:
- Özyinelemeli Yöntem(DFS): Her düğüm için, o düğümün sol ve sağ çocukları yer değiştirilir ve işlem rekürsif olarak alt ağaçlara uygulanır.
- Yinelemeli Yöntem (BFS): Bir kuyruk kullanılarak ağaç seviye seviye ziyaret edilir ve her düğümde çocuklar yer değiştirilir.
Code Özyinelemeli(DFS)
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def invertTree(self, root):
if not root:
return None
# Sol ve sağ alt ağaçları yer değiştir
root.left, root.right = root.right, root.left
# Rekürsif olarak sol ve sağ alt ağaçları ters çevir
self.invertTree(root.left)
self.invertTree(root.right)
return root
Code Yinelemeli (Breadth-First Search - BFS)
from collections import deque
class Solution:
def invertTree(self, root):
if not root:
return None
queue = deque([root])
while queue:
current = queue.popleft()
# Mevcut düğümün çocuklarını yer değiştir
current.left, current.right = current.right, current.left
# Çocukları sıraya ekle
if current.left:
queue.append(current.left)
if current.right:
queue.append(current.right)
return root
Complexity
- Time complexity (Zaman Karmaşıklığı): Her iki yöntem için de O(n), burada n ağaçtaki düğüm sayısıdır. Her düğüm bir kez işlenir.
- Space complexity (Alan Karmaşıklığı):
- Özyinelemeli için O(h), burada h ağacın yüksekliği (maksimum derinlik). Çağrı yığını bu kadar alan kullanır.
- Yinelemeli (BFS) için O(w), burada w ağacın en geniş seviyesindeki düğüm sayısıdır. Bu en kötü durumda ağacın yarısı olabilir.